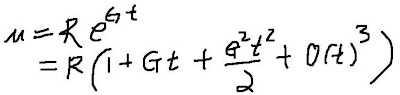Karin, Uri Alon, Senescent cell turnover slows with age -> Gompertz law

 

Karin19 Nat Communication used a threshold Xc of senescent cell to model death. 

In this saturation-removal (SR) model, X is the Senescent Cell (SnC) population. $\beta$ is the removal rate, $\eta$ is the constant self-decay rate, and $\keppa$ is the mid-point saturation point of SnC, and the last term is the noise.  Its seems to me that if we replace X with S, we might be able to approximate the Gompertz form. 

*** naked mole rat, non-aging model?

elife:

Naked mole-rat mortality rates defy

Gompertzian laws by not increasing with

age

J Graham Ruby, Megan Smith, Rochelle Buffenstein*

Calico Life Sciences LLC, South San Francisco, United States

TODO: exponential signal + white noises :: exponential fitting
Gompertiz signal + white noises :: exponential fitting vs Gompertz fitting. Perhaps, there is just not enough statistical power?

goodness of fit test, gompertz model

http://www.tandfonline.com/doi/abs/10.1080/03610926.2014.892323

robust statistics methods and measures

consistency

asymptotic bounds

cook's distance
https://en.wikipedia.org/wiki/Cook%27s_distance

M-estimator

Influence function and sensitivity curves

sir2, SIR2 overexpression, LRT

Conclusions: 

(1) sir2D and WT have different R and G. 

(2) sir2D and SIR2 overexpression share the same G. 

Black: by4742; Red: sir2D, Blue: SIR2-overexpression.

Gompertz versus Weibull, semilog versus log-log plot

Gompertz m = R exp(Gt)
    so, ln(m) = Gt  semi-log is linear.

Weibull     m = A t^(B)
   so, ln(m) = lnA + B ln(t)   log-log is linear.

Because Weibull takes an extra log-transformation, it 'suppresses' nosies in the data, therefore naturally fits bettern than Gomeprtz model.

flexsurv usage and results

fitGomp = flexsurvreg( formula=Surv(tb$rls) ~ 1, dist='gompertz')

> fitGomp$res
              est        L95%       U95%
shape 0.074024323 0.065724069 0.08232458

rate  0.009551328 0.007533154 0.01211018

fitGomp$coeff['rate'] has to be transformed by exp() function. 

Compare binomial, gompertz, and weibull model, fitting with simulated binomial-aging-model lifespan

# ~/0.network.aging.prj/0a.network.fitting/_binomial_aging20140711.r

#test binomial aging model
rm(list=ls());

source("lifespan.20131221.r")
require(flexsurv)


##### log likelihood function, 3-parameter binomial mortality rate model
# http://hongqinlab.blogspot.com/2013/12/binomial-mortailty-model.html
# m = R ( 1 + t/t0)^(n-1)
# s = exp( (R t0/n)*(1 - (1+t/t0)^n ) )  

llh.binomialMortality.single.run <- function( Rt0n, lifespan ) {
  I = Rt0n[1]; t0 = Rt0n[2]; n=Rt0n[3];
  my.data = lifespan[!is.na(lifespan)];
  log_s = (I * t0 /n )*(1 - (1 + my.data/t0)^n);
  log_m = log(I) +  (n-1) * log(1 + my.data/t0 ); 
  my.lh = sum(log_s)  + sum(log_m);
  print (Rt0n ); #trace the convergence
  ret = - my.lh # because optim seems to maximize 
}

#random number from binomial-aging model
rbinomial.aging <- function ( Rt0n, n){
    x.uniform = runif(n)
    inverse.binomialaging.CDF = function(R,t0,n,y) {t0*((1- n*log(y)/(R*t0))^(1/n) -1) }
    x.binomialaging = inverse.binomialaging.CDF(Rt0n[1],Rt0n[2], Rt0n[3], x.uniform)
    return(x.binomialaging)
}

set.seed(20140711)
x = rbinomial.aging( c(0.001,10, 5), 1000)
fitBinom = optim ( c(0.001,10, 3),  llh.binomialMortality.single.run , lifespan=x, 
              method="L-BFGS-B", lower=c(1E-10,0.05,1E-1), upper=c(10,100,50) );  

fitGomp = optim ( c(0.005, 0.08),  llh.G.single.run , lifespan=x,
                  method="L-BFGS-B", lower=c(1E-10,1E-2), upper=c(10,10) );  

fitWeib2 = flexsurvreg(formula = Surv(x) ~ 1, dist="weibull")
fitGomp2 = flexsurvreg(formula = Surv(x) ~ 1, dist="gompertz")
fitGomp2$coeff

c(-fitGomp$value, fitGomp2$loglik, fitWeib2$loglik, -fitBinom$value)

Flexsurv can over-fit the Gompertz with negative values, and Weibull gave the best value!!! 
Even though the random number are generated by binomial aging model, its fitting gave the lowest likelihood?!

TODO: I should to provide a gradient function for optim(method='L-BFGS-B')
Or try optimx()

For binomial-aging, $n$ is under-estimated by optim(), but $m0$ is over-estimated. When the entire data is fitted with Gompertz model, $G$ is too low. How about fitting within initial stage? 

set.seed(20140711)

x = round( rbinomial.aging( c(0.001,10, 4), 5000), digits=1 )#t0=10, n=4

tb = calculate.mortality.rate(x)

plot( tb$s ~ tb$t)

plot( tb$mortality.rate ~ tb$t )

plot( tb$mortality.rate ~ tb$t, log='y', main='linear for Gompertz' )

plot( tb$mortality.rate ~ tb$t, log='yx', main='linear for Weibull' )

set.seed(20140711)
x = rbinomial.aging( c(0.01,25, 4), 100)  #large m0, t0=25, n=4
x = round( x + 0.5, digits=0)
fitBinom = optim ( c(0.01,25, 3.5),  llh.binomialMortality.single.run , lifespan=x,
              method="L-BFGS-B", lower=c(1E-10,0.05,1E-1), upper=c(10,100,50) );

fitGomp = optim ( c(0.005, 0.08),  llh.G.single.run , lifespan=x,
                  method="L-BFGS-B", lower=c(1E-10,1E-2), upper=c(10,10) );

fitWeib2 = flexsurvreg(formula = Surv(x) ~ 1, dist="weibull")
fitGomp2 = flexsurvreg(formula = Surv(x) ~ 1, dist="gompertz")
fitGomp2$coeff

c(-fitGomp$value, fitGomp2$loglik, fitWeib2$loglik, -fitBinom$value)

Good, binomial aging model gives the best likelihood.

Plot confirmed that Gompertz looks better than Weibull. 

todo: Gomperz, Weibull variance comparison

Given the same mean lifespan, how are the variances of Gompertz and Weibull distribution? GG01 suggests that Weibull is the default model and Gompertz is the derived one. They also argue that it is the initial stage are different.

A technical problem is the tail part. Do the models comparison in practice basically differ in the tails?

We do similar study.
1. Simulate Gompertz random variables and compare AIC with Gompertz and Weibull.

2. Simulate Weibull random variables and compare AIC with Gompertz and Weibull.

3. Use linear fitting to check the initial stages.

Useful links: Weibull random number generator
http://stat.ethz.ch/R-manual/R-patched/library/stats/html/Weibull.html

Network configuration on gompertz and weibull fitting (need follow up)

When p=0.6, pop=2000, original GINDIP fits much better to Gompertz with regards to Weibull, as compared to the ms02 permutated network. 

I need to generate a distribution using 100 ms02 networks.

rgompertz, Gompertz random number

##########################################
#inverse of gompertz CDF
# see http://hongqinlab.blogspot.com/2013/06/median-lifespan-of-2-parameter-gompertz.html
#inverse.gomp.CDF = function(R,G,y) {  (1/G)*log(1 - (G/R)*log(1-y)  ) }

#see generate random number with a given distribution
# http://hongqinlab.blogspot.com/2013/12/generate-gompertz-random-numbers.html

#generate Gompertz random numbers
rgompertz = function(R,G, n){
  x.uniform = runif(n)
  inverse.gomp.CDF = function(R,G,y) {  (1/G)*log(1 - (G/R)*log(1-y)  ) }
  x.gompertz = inverse.gomp.CDF(0.001,0.2, x.uniform)
  return(x.gompertz)
}
rgompertz(0.001,0.2,100)

Use simulated Gompertz random number to test flexsurv Gompertz and Weibull fitting results

Summary: I experimented the sample size. For 50 cells, the Gompertz model may be the better fit 4 out of 5 times. For 100 cells, Gompertz is better than Weibull maybe 9 out of 10 times. For 500 cells, Gompertz is always bettern than the Weibull model.

Conclusion: For most yeast life span assay, it is not always easy to tell whether Gompertz or Weibull is a better fit.

Comments: The actual results probably also depend on R and G, which determine the variance.

code: 20131221.gompertz.simulation.R


# generate gompertz random numbers
# fit with flexsurv Gompertz and weibull models

#inverse of gompertz CDF
# see http://hongqinlab.blogspot.com/2013/06/median-lifespan-of-2-parameter-gompertz.html
inverse.gomp.CDF = function(R,G,y) {  (1/G)*log(1 - (G/R)*log(1-y)  ) }

#see generate random number with a given distribution
# http://hongqinlab.blogspot.com/2013/12/generate-gompertz-random-numbers.html

x.uniform = runif(60)
hist(x.uniform)

x.gompertz = inverse.gomp.CDF(0.001,0.2, x.uniform)
hist(x.gompertz)

summary(x.gompertz)

source("lifespan.r")
tb = calculate.s(x.gompertz)
plot(tb$s ~ tb$t)

require(flexsurv)
require(flexsurv)
lifespan = x.gompertz
lifespanGomp = flexsurvreg(formula = Surv(lifespan) ~ 1, dist = 'gompertz')  
lifespanWeib = flexsurvreg(formula = Surv(lifespan) ~ 1, dist = 'weibull')  

c(lifespanWeib$AIC, lifespanGomp$AIC, lifespanWeib$AIC - lifespanGomp$AIC )

Generate random numbers with a given distribution

This is related to generating random numbers from arbitrary distributions.  Basically, inverse of an uniform random number can be used.

From: http://www.ece.virginia.edu/mv/edu/prob/stat/random-number-generation.pdf


See also
http://epub.ub.uni-muenchen.de/1716/1/paper_338.pdf

What is the inverse function of Gompertz and Weibull distribution?

Taylor expansion of Gompertz function

Note that exp(G t=0)=1. 
Derivatives of u(t) near t=0 can be found by chain rules:

Reference:
http://en.wikipedia.org/wiki/Taylor_series

Results repeated in Mathematica:

flexsurv, R package,

R package 'flexsurv' provides optim() based parametric fitting. Two parameter Gomertz and Weibull model are included.  The 'flexsurv' use Hessian to build confidence intervals around the maximum likelihood estimate.

I did not see an obvious way to do nested model test using 'flexsurv'.

Witten 1985 MAD, critical elements in a graph and Gompertz model

Witten 1985, Mech Ageing and Dev. 1985.

Witten85 used $R(t)$ as the survival function. $h_0$ as the initial mortality rate, $\gamma$ as the Gompertz coefficient.  Witten85 seems to treat probability = reliability (page 142), which is different from Leemis's approach.

Witten85 assumed $m$ critical components in a graph model of a cell. There existed a critical number $m_c$ that is the threshold for the system (cell) to fail. This is equivalent to the parallel block configuration used by GG01.

Witten85 used Markov transitional states to model the failure of each critical component $M*$.  I did not see how  these transitional states are used for his derivation of the Gompertz model.

Witten85 used 'deviation' concept from Witten83. Witten85 assumes exponential failure function for each critical component (page 148), similar to GG01. It seems that although 'deviation' argument was used, it was not incorporated into the building toward Gompertz model.

In Eq 21, Witten85 shows that system viability (reliability) $R_SYS$ is basically the viability function of a serial system. Witten85 assumed a 'critical time' $t*$ (page 148), and approximate the binomial form in Eq 21 to obtain the Gompertz form using the exactly approximation used by GG91. 

It is perplexing to me that Eq21 shows a serial configuration (based on Eq 14), but Witten85 argues for parallel configuration in Eq 13.  For serial system, the product form also means that any single failure of the critical components will lead to system failure.  If 'all of the critical elements must fail' for a system to fail, it should be a parallel configuration.

Witten85 introduced 'cost' in Eq 30 on page 152: Cost ~ m^beta, where $m$ is the number of critical elements.

*** Two-parameter Gompertz model

Median lifespan of the 2-parameter

Survivorship

The Gompertz model in 'flexsurv' is

Notice that pdf = mortality rate * (1-s)  
pdf = mortality rate * s (based on mortality definition)
 m = - 1/s ds/dt  , so - ds/dt = pdf = m * s

So, flexsurv-shape a ==G, flexsurv rate b = R. 

Inverse of Gompertz CDF:

Verify optim() estimation using 2 and 3 parameter Gompertz model.

Using 2 and 3 parameter Gompertz model. When M is large, ignoring M will inflate I, the initial mortality rate. 




rm(list=ls())
source("/Users/hongqin/lib/R/lifespan.r")

##two parameter Gompertz model 
N=1000
I =0.005
G = 0.10
t= seq(1, 100, by=1)
s = G.s(c(I,G,0), t)
plot( s ~ t)
mu = I * exp(G*t)
plot ( s*mu ~ t )
pmf = s * mu  # prob mass function
pmf = pmf / sum(pmf)
summary ( pmf * N)
hist( round( pmf * N) )
lifespanT = rep( t, round(pmf*N))
hist(lifespanT, br=20)
summary(lifespanT)


##### log likelihood function, simple gompertz mortality model
#s = exp( (I/G) *(1 - exp(G* my.data)) )  ;
#m = I * exp( G * my.data );   
llh.gompertz.single.run <- function( IG, lifespan, trace=0 ) {
  #print(IG)
  I = IG[1]; G = IG[2]; 
  my.data = lifespan[!is.na(lifespan)];
  log_s = (I/G) *(1 - exp(G* my.data))
  #if( I< 0 ) { I = 1E-10 }
  log_m = log(I) +  G * my.data ; 
  my.lh = sum(log_s)  + sum(log_m);
  if (trace) {
    print (IG ); #trace the convergence
  }
  ret = - my.lh # because optim seems to maximize 
}

lifespan = sample(lifespanT, 30)
shat = calculate.s( lifespan )
plot(shat$s ~ shat$t )

ret1a = optim ( c(I,G)*2, fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1a$par / c(I,G)

ret1a = optim ( c(I, G), fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1a$par / c(I,G)

ret1b = optim ( c(I, G)*c(0.01, 1.5), fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1b$par / c(I,G)

ret1c = optim ( c(I,G)*c(0.01,1.5), fn=llh.gompertz.single.run, lifespan=lifespan, trace=1  );
ret1c$par / c(I, G)

ret1d = optim ( c(0.05, 0.15), fn=llh.gompertz.single.run, lifespan=lifespan, trace=1  );
ret1d$par / c(I,G)

ret1e = optim ( c(0.05, 0.1), fn=llh.gompertz.single.run, lifespan=lifespan  );
ret1e$par / ret1d$par

#################
## 3  parameter Gompertz model 
N=1000
I =0.005
G = 0.10
M = 0.05

t= seq(1, 100, by=1)
s = GM.s(c(I,G,0), t)
plot( s ~ t)

mu = I * exp(G*t) + M

plot ( s*mu ~ t )
pmf = s * mu  # prob mass function
pmf = pmf / sum(pmf)
summary ( pmf * N)
hist( round( pmf * N) )
lifespanT = rep( t, round(pmf*N))
hist(lifespanT, br=20)
summary(lifespanT)



lifespan = sample(lifespanT, 30)
shat = calculate.s( lifespan )
plot(shat$s ~ shat$t )

ret1a = optim ( c(I,G, M)*2, fn=llh.GM.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1a$par / c(I,G, M)


ret1b = optim ( c(I, G), fn=llh.G.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1b$par / c(I,G)
#ignore larger M can inflate R



ret1b = optim ( c(I, G)*c(0.01, 1.5), fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1b$par / c(I,G)

ret1c = optim ( c(I,G)*c(0.01,1.5), fn=llh.gompertz.single.run, lifespan=lifespan, trace=1  );
ret1c$par / c(I, G)

ret1d = optim ( c(0.05, 0.15), fn=llh.gompertz.single.run, lifespan=lifespan, trace=1  );
ret1d$par / c(I,G)

ret1e = optim ( c(0.05, 0.1), fn=llh.gompertz.single.run, lifespan=lifespan  );
ret1e$par / ret1d$par

Investigate optim() by simulation of two parameter Gompertz model

To see how optim() works in R, I tested it using simulated data. Method L-BFGS-B appears to give the most accurate fitting result. For methods tested, the initial values seem to really influence the accuracy of the fitting result.



rm(list=ls())
source("/Users/hongqin/lib/R/lifespan.r")
N=1000
I =0.005
G = 0.10
t= seq(1, 100, by=1)
s = G.s(c(I,G,0), t)
plot( s ~ t)
mu = I * exp(G*t)
plot ( s*mu ~ t )
pmf = s * mu  # prob mass function
pmf = pmf / sum(pmf)
summary ( pmf * N)
hist( round( pmf * N) )
lifespanT = rep( t, round(pmf*N))
hist(lifespanT, br=20)
summary(lifespanT)


##### log likelihood function, simple gompertz mortality model
#s = exp( (I/G) *(1 - exp(G* my.data)) )  ;
#m = I * exp( G * my.data );  
llh.gompertz.single.run <- function( IG, lifespan, trace=0 ) {
  #print(IG)
  I = IG[1]; G = IG[2];
  my.data = lifespan[!is.na(lifespan)];
  log_s = (I/G) *(1 - exp(G* my.data))
  #if( I< 0 ) { I = 1E-10 }
  log_m = log(I) +  G * my.data ;
  my.lh = sum(log_s)  + sum(log_m);
  if (trace) {
    print (IG ); #trace the convergence
  }
  ret = - my.lh # because optim seems to maximize
}

lifespan = sample(lifespanT, 30)
shat = calculate.s( lifespan )
plot(shat$s ~ shat$t )

ret1a = optim ( c(I,G)*2, fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1a$par / c(I,G)

ret1a = optim ( c(I, G), fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1a$par / c(I,G)

ret1b = optim ( c(I, G)*c(0.01, 1.5), fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1b$par / c(I,G)

ret1c = optim ( c(I,G)*c(0.01,1.5), fn=llh.gompertz.single.run, lifespan=lifespan, trace=1  );
ret1c$par / c(I, G)

ret1d = optim ( c(0.05, 0.15), fn=llh.gompertz.single.run, lifespan=lifespan, trace=1  );
ret1d$par / c(I,G)

ret1e = optim ( c(0.05, 0.1), fn=llh.gompertz.single.run, lifespan=lifespan  );
ret1e$par / ret1d$par

R code for nested model test, likelihood ratio test, using AgingData 0517.xls

2013 Nov 6 Note: Permutation based test are probably more 'accurate' at estimating p-values than Chi-square. 


rm( list=ls())
list.files()

file = "AgingData_0517.csv"
tb = read.csv( file );


##### log likelihood function, simple gompertz mortality model
   #s = exp( (I/G) *(1 - exp(G* my.data)) )  ;
   #m = I * exp( G * my.data );  
 llh.gompertz.single.run <- function( IG, lifespan ) {
   #print(IG)
   I = IG[1]; G = IG[2];
   my.data = lifespan[!is.na(lifespan)];
   log_s = (I/G) *(1 - exp(G* my.data))
   if( I< 0 ) { I = 1E-10 }
   log_m = log(I) +  G * my.data ;
   my.lh = sum(log_s)  + sum(log_m);
   print (IG ); #trace the convergence
   ret = - my.lh # because optim seems to maximize
 }

#####

ret1a = optim ( c(0.0034, 0.1), fn=llh.gompertz.single.run, lifespan=tb[,1], lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1b = optim ( c(0.05, 0.2), fn=llh.gompertz.single.run, lifespan=tb[,1], lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1c = optim ( c(0.039, 0.1), fn=llh.gompertz.single.run, lifespan=tb[,1]  );
ret1d = optim ( c(0.05, 0.15), fn=llh.gompertz.single.run, lifespan=tb[,1]  );
ret1c$par / ret1d$par
ret1e = optim ( c(0.1, 0.1), fn=llh.gompertz.single.run, lifespan=tb[,1]  );
ret1e$par / ret1d$par

#set up a template for fitting parameters
label = c("R","G", "mean", "median", "stddev", "CV", 'p_wilcox', 'p_ks')
allFitPar = data.frame( matrix(NA, nrow=length(label), ncol=length(tb[1,])) )
rownames(allFitPar) = label
names(allFitPar) = names(tb)

 
#loop over
for (col in names(tb)) {
  cur_lifespan = tb[,col]
  retTmp = optim ( c(0.039, 0.1), fn=llh.gompertz.single.run, lifespan=cur_lifespan  );
  allFitPar[1:2, col] = retTmp$par
  allFitPar["mean", col] = mean(cur_lifespan, na.rm=T)
  allFitPar["median", col] = median(cur_lifespan, na.rm=T)
  allFitPar["stddev", col] = sqrt( var(cur_lifespan, na.rm=T))
  allFitPar["CV", col] = allFitPar["stddev", col] / allFitPar["mean", col]
  tmp = wilcox.test( tb[,'wt'], tb[,col] ) 
  allFitPar['p_wilcox', col] = tmp$p.value
  tmp2 = ks.test( tb[,'wt'], tb[,col] ) 
  allFitPar['p_ks', col] = tmp2$p.value
 
}
allFitPar


#################################
##### LRT
### 1) model H0, same G and same I
### 2) model H1i, same G, different I
### 3) model H1g, different G, same I
### 4) model H2, different G, different I
                                  #    I1       G1       I2         G2
 H0  <- function( rawIG ) { IG <- c(rawIG[1], rawIG[2], rawIG[1], rawIG[2] ) }  #all the same
 H1i <- function( rawIG ) { IG <- c(rawIG[1], rawIG[2], rawIG[3], rawIG[2] ) }  #different I
 H1g <- function( rawIG ) { IG <- c(rawIG[1], rawIG[2], rawIG[1], rawIG[4] ) }  # different G
 H2  <- function( rawIG ) { IG <- c(rawIG[1], rawIG[2], rawIG[3], rawIG[4] ) }  # all different

 Hx.llh.gompertz.single.run <- function( rawIG, model, lifespan1, lifespan2 ) {
   IG = model(rawIG);
   I1 = IG[1]; G1 = IG[2]; I2 = IG[3]; G2 = IG[4];
   my.data1 = lifespan1[!is.na(lifespan1)];
   my.data2 = lifespan2[!is.na(lifespan2)];
   log_s1 = (I1/G1) *(1 - exp(G1* my.data1))
   log_s2 = (I2/G2) *(1 - exp(G2* my.data2))
   log_m1 = log(I1) +  G1 * my.data1 ;
   log_m2 = log(I2) +  G2 * my.data2 ;
   my.lh = sum(log_s1) + sum(log_m1) + sum(log_s2) + sum(log_m2)
   print (IG ); #trace the convergence
   ret = - my.lh # because optim seems to maximize
 }

## LRT to exam whether wt, wtCR share the same G, I
llh.H0   = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H0,   lifespan1=tb$wt, lifespan2=tb$wtCR );
llh.H1i  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1i,  lifespan1=tb$wt, lifespan2=tb$wtCR );
llh.H1g  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1g,  lifespan1=tb$wt, lifespan2=tb$wtCR );
llh.H2  = optim( c(0.01,0.2,0.01,0.1),   Hx.llh.gompertz.single.run, model=H2,  lifespan1=tb$wt, lifespan2=tb$wtCR );

cbind(llh.H0$par, llh.H1i$par, llh.H1g$par, llh.H2$par);

LH = c(llh.H0$value, llh.H1i$value, llh.H1g$value, llh.H2$value);
LH
deltaLH =  - LH + llh.H0$value;
deltaLH
1 - pchisq( 2*deltaLH, df =c(1,1,1,2) );
#p=0.06 not significant for all models.

#################################
###### End of LRT    ############
#################################

## LRT to exam whether ybr053cD, and CR share the same G, I
llh.H0   = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H0,   lifespan1=tb[,3], lifespan2=tb[,4] );
llh.H1i  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1i,  lifespan1=tb[,3], lifespan2=tb[,4] );
llh.H1g  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1g,  lifespan1=tb[,3], lifespan2=tb[,4] );
llh.H2   = optim( c(0.01,0.2,0.01,0.1),   Hx.llh.gompertz.single.run, model=H2,  lifespan1=tb[,3], lifespan2=tb[,4] );

cbind(llh.H0$par, llh.H1i$par, llh.H1g$par, llh.H2$par);

LH = c(llh.H0$value, llh.H1i$value, llh.H1g$value, llh.H2$value);
LH
deltaLH =  - LH + llh.H0$value;
deltaLH
1 - pchisq( 2*deltaLH, df =c(1,1,1,2) );
#[1] 1.00000000 0.01498437 0.01368829 0.04515191

#################################
###### End of LRT    ############
#################################

## LRT to exam whether ybr053cD, and CR share the same G, I
llh.H0   = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H0,   lifespan1=tb[,5], lifespan2=tb[,6] );
llh.H1i  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1i,  lifespan1=tb[,5], lifespan2=tb[,6] );
llh.H1g  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1g,  lifespan1=tb[,5], lifespan2=tb[,6] );
llh.H2   = optim( c(0.01,0.2,0.01,0.1),   Hx.llh.gompertz.single.run, model=H2,  lifespan1=tb[,5], lifespan2=tb[,6] );
cbind(llh.H0$par, llh.H1i$par, llh.H1g$par, llh.H2$par);

LH = c(llh.H0$value, llh.H1i$value, llh.H1g$value, llh.H2$value);
LH
deltaLH =  - LH + llh.H0$value;
deltaLH
1 - pchisq( 2*deltaLH, df =c(1,1,1,2) );
#[1] 1.00000000 0.04595566 0.31817030 0.04188332

#################################
###### End of LRT    ############
#################################


## LRT to exam whether ybr053cD, and CR share the same G, I
llh.H0   = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H0,   lifespan1=tb[,7], lifespan2=tb[,8] );
llh.H1i  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1i,  lifespan1=tb[,7], lifespan2=tb[,8] );
llh.H1g  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1g,  lifespan1=tb[,7], lifespan2=tb[,8] );
llh.H2   = optim( c(0.01,0.2,0.01,0.1),   Hx.llh.gompertz.single.run, model=H2,  lifespan1=tb[,7], lifespan2=tb[,8] );

cbind(llh.H0$par, llh.H1i$par, llh.H1g$par, llh.H2$par);

LH = c(llh.H0$value, llh.H1i$value, llh.H1g$value, llh.H2$value);
LH
deltaLH =  - LH + llh.H0$value;
deltaLH
1 - pchisq( 2*deltaLH, df =c(1,1,1,2) );
#[1] 1.00000000 0.04595566 0.31817030 0.04188332

#################################
###### End of LRT    ############
#################################