*** H2O2 induced LOH ~ ARLS: Tradeoff between robustness and replicative lifespan

------
2013Dec5 comments
M2-8 has a dilution bias and was not fitted correctly in this plot.
M32 is a tricky strain that we repeated at least 5 times.
----------

Large Cv/Cb indicate better survival ship beyond H2O2-induced LOH. The negative correlation indicates a trade off
between Cv/Cb and RLS. 

plot( tb$Cv.vs.Cb ~ tb$ARLS, pch=19, col="red", main="H2O2-LOH ~ ARLS, 20130531" )
 text( tb$ARLS, tb$Cv.vs.Cb, tb$strain)
 m = lm(tb$Cv.vs.Cb ~ tb$ARLS )
 abline( m, col="blue")
 summary(m)
 text(33, 3, "R2=0.37 p=0.035")

Small L0 indicates better asymmetry. Large Cv/Cb indicates better tolerance to H2O2 or
more sensitive to H2O2. So, this negative correlation actually indicates a positive relationship
between Cv/Cb and mitotic asymmetry. 

 plot( tb$Cv.vs.Cb ~ tb$L0.all , pch=19, col="red", main="H2O2-LOH ~ mitotic asymmetry, 20130531" )
 text( tb$L0.all, tb$Cv.vs.Cb, tb$strain)
 m = lm(tb$Cv.vs.Cb ~ tb$L0.all )
 abline( m, col="blue")
 summary(m)
 text(0.2, 3.5, "R2=0.42 p=0.031")

Updated on 2013 June 18. I switched x-y axis for more clear presentation.

Updated on 2013 June 18.

Conclusions:  
 Cv/Cb ~(-)~ ARLS
 Tc/Tg ~(-)~ ARLS
  G       ~(-)~ ARLS
Morphological robustness ~(-)~ RLS ?
Growth fitness ~(+)~ RLS ?


Reference:
_2013May31-H2O2LOH.R
_2013June18-H2O2LOH.R

Loop over all columns for exploratory regression analysis in R

### all possible regression analysis for a given column
pTb = 1: length(tb[1,])
names(pTb) = names(tb)
 for( j in c(2:15,17:34) ) {
   m = lm( tb[, j] ~ tb$Cv.vs.Cb)
   sm = summary(m)
   pTb[j] = 1 - pf(sm$fsta[1], sm$fsta[2], sm$fsta[3])
 }
 pTb[pTb<0.05]


pTb[pTb<0.05]
         ARLS          Lmax        L0.all     CLS.vs.Tc      Cv.vs.Cb      Cb.vs.Cv 
 3.546097e-02  3.877701e-02  3.137392e-02  4.748623e-02  0.000000e+00  7.306331e-05 
Cb.vs.Cv.mean 
 5.729385e-04 

Compare manually estimated Cv, Cb ~ gnls estimations

Mid-point of H2O2-dependent viability can be consistently estimated manually and by gnls. 

These are the fitting results of H2O2-LOH data.

Comparison of manually fitted Cb ~ gnls results. Red line is y=x, blue line is the model of gnls_Cb = a*manualCb + b. 

Gnls seem to give larger Cb than manual estimations. So, I should use manual estimations as initial values for 'gnls' and see whether it helps. Function 'gnls' treats all points equally correct, but I know data points in higher H2O2 concentration are more noisy due to fewer colonies. So, manual fit has some advantage, though 'gnls' can be viewed as kind of 'objective' method (well, if initial values are not considered as human biases).



# I am concerned how initial values can influence Cb estimation.
# The black colonies data are very noisy, so initial values can trapped fitting to different local optima.

rm(list=ls())
setwd("~/github/LOH_H2O2_2012-master/analysis")
files = list.files(path="../", pattern="_*csv")

tb29 = read.csv("../_ctl.tb_out.20130529.csv")
tb30 = read.csv("../_ctl.tb_out.20130530a.csv")
tb30$files = as.character(tb30$files)

head(tb29)
head(tb30)
tb30$change = tb30$Cb / tb29$Cb
summary(tb30)

tb30$color = ifelse(tb30$change>1.5 | tb30$change<0.5, "red", "black"   )
tb30$pch = ifelse(tb30$change>1.5 | tb30$change<0.5, 19, 1   )
plot( tb29$Cb ~ tb30$Cb, xlim=c(0,0.4),pch=tb30$pch, col=tb30$color)

tb30$label = ifelse(tb30$change>2 | tb30$change<0.5, as.character(tb30$files), NA   )
text( tb30$Cb, tb29$Cb, tb30$label)

red= tb30[tb30$color=='red', ]
head(tb30)
tb30$Cv.vs.Cb = tb30$Cv / tb30$Cb

######load the manual fitting results
tbManual = read.csv("H2O2_Log_Plot_Summarized_data,2013May30.csv")
head(tbManual)
names(tbManual)=c("files", "Date", "strains", "Cv", "Cb", "OD600", "note")
tbManual$files = as.character(tbManual$files)

tbManual$Cv.vs.Cb = tbManual$Cv / tbManual$Cb

summary(tbManual$Cv.vs.Cb)
summary(tb30$Cv.vs.Cb)
tbManual[tbManual$Cv.vs.Cb>5, ]
str(tbManual)

### merge
intersect( tbManual$files, tb30$files )
head(tbManual)
head(tb30)

tmp = tbManual[match(tb30$files, tbManual$files), ]
cbind( tmp[,1], tb30[,1]) #visual check, passed. 

tb30M = data.frame( cbind( tb30, tmp[, c(2:9)]) )
head(tb30M)
plot( Cv.vs.Cb ~ Cv.vs.Cb.1, data=tb30M)

plot( Cv ~ Cv.1, data=tb30M, xlab="manual fit Cv", ylab="gnls Cv")

plot( Cb ~ Cb.1, data=tb30M, xlab= "manual Cb", ylab="gnls Cb")
x = seq(0,1, by=0.1); y = x; 
lines( y ~ x, col='red')
m = lm( Cb ~ Cb.1, data=tb30M)
summary(m)
abline(m, col='blue')

Eigenvector centrality for network analysis

Wikipedia gives a succinct explanation for the eigenvector centrality measure. Basically the centrality score of vertex $v$ is

where $a_{v,t}$ is an element of the adjacency matrix $A$ with a value of 1 for connection between $v$ and $t$, and 0 for no direct connection between $v$ and $t$.  We can move $\lambda$ to the left side of the above equation, and substitutie elements with vector and matrix,

Hence, $\lambda$ is the eigen value of matrix $A$. 

One of my nagging question is why it is sufficient to focus only on the greatest eigen value. According to Wikipedia entry, because all the elements in the eigen vector ought to be positive, the Perron-Frobenius theorem indicates that only the greatest eigen value can satisfy this requirement. Elements in the corresponding dominant eigen vector (I am not sure of this term) give the centrality measure for each row (vertice). 

Wikipedia mentions that matrix $A$ can be generalized to weighted matrix. 

Reference: 

http://en.wikipedia.org/wiki/Eigenvector_centrality#Eigenvector_centrality

Perron–Frobenius theorem

LOH and robustness, Tc/Tg ~ ln(R) + G, Strehler-Mildvan correlation in wild yeast

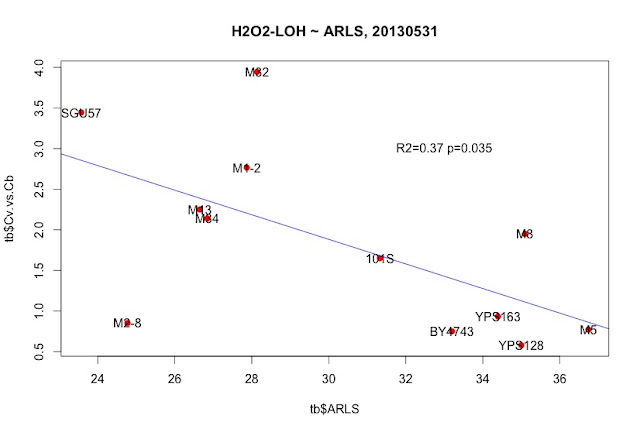
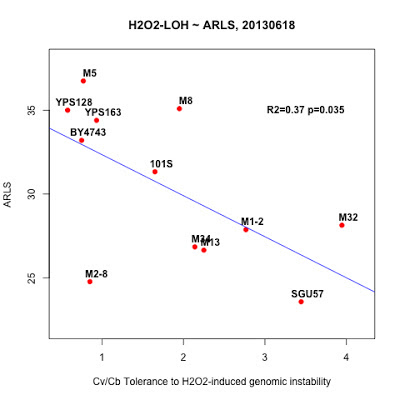
"_2013May29,R0-G-TcTg.regression.by.mean.R" in  /Users/hongqin/projects/LOH_H2O2_2012-master/analysis. The ARLS data is from Qin06EXG. 


 rm( list = ls() );
 tb = read.table("summary.new.by.strain.csv", header=T, sep="\t");
 tb.old = tb;
 labels = names( tb.old );
 #tb = tb.old[c(1:11), c(1:5,8, 10, 12, 14, 16, 18, 20, 22)]

 tb = tb.old[c(1:11), c("strain","ARLS","R0","G","CLS","Tc", "Tg","Tmmax","Tbmax", "Td", "Tdmax","TLmax","Lmax", 
 "b.max", "b.min", "strains", "L0.all", "L0.small" , "Pbt0","Pb0.5t0", "Pbt0.b") ];

 tb$CLS.vs.Tc = tb$CLS / tb$Tc; 
 tb$Tg.vs.Tc = tb$Tg / tb$Tc;
 tb$Tc.vs.Tg = tb$Tc / tb$Tg

> summary( lm( tb$Tc.vs.Tg ~ log(tb$R0) + tb$G  ) )

Call:

lm(formula = tb$Tc.vs.Tg ~ log(tb$R0) + tb$G)

Residuals:

     Min       1Q   Median       3Q      Max 

-0.16512 -0.04416 -0.01631  0.03805  0.22175 

Coefficients:

            Estimate Std. Error t value Pr(>|t|)   

(Intercept)  1.58691    0.31955   4.966  0.00110 **

log(tb$R0)   0.22037    0.06505   3.388  0.00953 **

tb$G         4.68078    1.68987   2.770  0.02430 * 

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

Residual standard error: 0.1101 on 8 degrees of freedom

Multiple R-squared: 0.5991, Adjusted R-squared: 0.4989 

F-statistic: 5.977 on 2 and 8 DF,  p-value: 0.02584 

require(scatterplot3d);
s3d <- scatterplot3d( log(tb$R0), tb$G, tb$Tc.vs.Tg,  type='h',color="red", pch=16,
                      main="Correlations among Tc/Tg, log(R0), and G", 
                      angle=40, scale.y=0.7
);
my.lm <- lm( tb$Tc.vs.Tg ~ log(tb$R0) + tb$G);
s3d$plane3d( my.lm, lty.box="solid");

text(s3d$xyz.convert( tb$Tc.vs.Tg, log(tb$R0), tb$G), labels=tb$strain, pos=1)

> model = lm(log(tb$R0) ~ tb$G )
> summary( model ) #p=0.02, strehler-mildvan correlation!

Call:
lm(formula = log(tb$R0) ~ tb$G)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.86676 -0.45345 -0.04328  0.40139  0.80255 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -4.2158     0.8407  -5.015 0.000724 ***
tb$G        -17.2886     6.4637  -2.675 0.025425 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

Residual standard error: 0.5641 on 9 degrees of freedom
Multiple R-squared: 0.4429, Adjusted R-squared: 0.381 

F-statistic: 7.154 on 1 and 9 DF,  p-value: 0.02543 
> plot( log(tb$R0) ~ tb$G, pch=19, ylim=c(-8, -5), xlim=c(0.07, 0.17) )
> title("p=0.025, Strehler-Mildvan, natural isoaltes")
> text( tb$G*1.01, log(tb$R0)*1.02, tb$strain)
> abline(model, col='red')

> tb

   strain     ARLS        R0         G       CLS       Tc        Tg     Tmmax     Tbmax        Td     Tdmax     TLmax      Lmax      b.max

1    101S 31.32761 0.0012098 0.1421899  3.393531 4.580000  5.686667  5.483333  5.633333  4.786667  4.786667  6.653333 2.4900000 0.04333333

2    M1-2 27.86968 0.0024437 0.1283620 10.370586 6.273333  6.930000  7.316667  6.833333  6.930000  6.930000  7.653333 0.7066667 0.04000000

3     M13 26.65020 0.0029551 0.1252717 16.273320 8.010000 11.053333  9.433333 11.083333  9.246667  9.246667  9.666667 0.6533333 0.13666667

4     M14 36.58444 0.0018812 0.0949553  7.212224 3.960000  7.043333  4.900000  7.016667  5.840000  5.840000  9.500000 1.2000000 0.16333333

5    M2-8 24.77079 0.0041838 0.1193465  4.124016 4.122500  4.507500  5.100000  4.487500  5.870000  5.870000  7.020000 3.3450000 0.03425000

6     M32 28.13750 0.0017568 0.1417765  6.422428 7.963333  7.413333  9.733333  7.350000  8.206667  8.206667  7.626667 0.5966667 0.03000000

7     M34 26.84275 0.0012919 0.1629953  5.167521 6.732500  8.212500  8.325000  8.300000  8.382500  8.382500  7.552500 0.7925000 0.22250000

8      M5 36.74289 0.0040310 0.0681621  4.934625 5.920000  7.816667  7.050000  7.833333  6.546667  6.546667  6.906667 1.8400000 0.24333333

9      M8 35.09139 0.0003775 0.1619232 10.492830 6.783333 11.466667  8.216667 11.516667  6.026667  6.026667  6.873333 1.2400000 0.16666667

10 YPS128 34.99853 0.0011183 0.1209893  3.309616 8.630000 12.873333 10.750000 12.450000 11.420000 11.420000 11.766667 1.7333333 0.20666667

11 YPS163 34.39308 0.0008251 0.1350900  4.184502 5.246667  8.310000  6.850000  8.283333  7.140000  7.140000  5.246667 1.3266667 0.16333333

        b.min strains     L0.all   L0.small       Pbt0    Pb0.5t0     Pbt0.b CLS.vs.Tc  Tg.vs.Tc  Tc.vs.Tg

1  0.00000000    101S 0.15957447 0.09523810 0.00280093 0.00026676 0.00277755 0.7409457 1.2416303 0.8053927

2  0.00000000    M1-2 0.06164384 0.03571429 0.00183932 0.00006569 0.00189366 1.6531221 1.1046759 0.9052429

3  0.00000000     M13 0.09345794 0.12500000 0.00197697 0.00024712 0.00214845 2.0316255 1.3799417 0.7246683

4  0.00333333     M14 0.11224490 0.10975610 0.00699718 0.00076798 0.00660394 1.8212687 1.7786195 0.5622338

5  0.00000000    M2-8 0.14859438 0.16363636 0.00366569 0.00059984 0.00390693 1.0003677 1.0933899 0.9145868

6  0.01000000     M32 0.10962567 0.13440860 0.01235470 0.00166058 0.01252386 0.8065000 0.9309334 1.0741906

7  0.00250000     M34 0.17134831 0.16176471 0.00727065 0.00117614 0.00688487 0.7675486 1.2198292 0.8197869

8  0.00000000      M5 0.17187500 0.17948718 0.00200535 0.00035993 0.00206424 0.8335515 1.3203829 0.7573561

9  0.00000000      M8 0.05810398 0.07471264 0.00637153 0.00047603 0.00633754 1.5468545 1.6904177 0.5915698

10 0.01333333  YPS128 0.18353175 0.09166667 0.01086710 0.00099615 0.01106367 0.3835013 1.4916956 0.6703780

11 0.00666667  YPS163 0.25268817 0.09032258 0.00712283 0.00064335 0.00824009 0.7975545 1.5838628 0.6313678

Github for H2O2-LOH project, using snow leopard osX (large file)

I created a repository on GitHub website, then download the ZIP template directory, and find out the https site. 


ace:LOH_H2O2_2012-master hongqin$ pwd

/Users/hongqin/projects/LOH_H2O2_2012-master

$ git add *
$ git add H2O2_Log_Plot_Summarized_data,2012July24.xlsx 
$ git add analysis

$ git add data.H2O2-LOH

$ git commit -m "first H2O2-LOH"
#Many files are shown. 

$git remote add origin https://github.com/hongqin/LOH_H2O2_2012.git

$ git push --force origin master 

Username for 'https://github.com': hongqin

Password for 'https://hongqin@github.com': 

Counting objects: 498, done.

Delta compression using up to 2 threads.

Compressing objects: 100% (491/491), done.

Writing objects: 100% (498/498), 1.94 MiB | 996 KiB/s, done.

Total 498 (delta 215), reused 0 (delta 0)

Unable to rewind rpc post data - try increasing http.postBuffer  #An error here

error: RPC failed; result=65, HTTP code = 401

fatal: The remote end hung up unexpectedly

fatal: The remote end hung up unexpectedly

Everything up-to-date

To fix the http.postBuffer problem (default is 1M), see 

http://blog.lukebennett.com/2011/07/25/git-broken-pipe-error-when-pushing-to-a-repository/

$ git config http.postBuffer 209715200
$ git push --force origin master 
Username for 'https://github.com': hongqin
Password for 'https://hongqin@github.com': 
Counting objects: 498, done.
Delta compression using up to 2 threads.
Compressing objects: 100% (491/491), done.
Writing objects: 100% (498/498), 1.94 MiB, done.
Total 498 (delta 214), reused 0 (delta 0)
To https://github.com/hongqin/LOH_H2O2_2012.git
 + 9315588...47f5205 master -> master (forced update)

Check Github and now see the synced files.  

Uninstall WACOM driver and application for Bamboo tablet pen to avoid overheating a Snow Leopard laptop

I found the Wacom Tablet Driver overuse CPU and cause my snow leopard laptop to overheat. Hence, I decide to remove the Bamboo tablet application and drive.

I first moved /Application/Bamboo/ and /Application/Bamboo Dock to a different folder. I then shutdown and restart laptop, and found the Tablet driver is still running.

$ ps -ef | grep Tab
  501   241   215   0   0:00.04 ??         0:00.16 /Library/Application Support/Tablet/PenTabletDriver.app/Contents/MacOS/PenTabletDriver
  501   269   215   0   0:00.02 ??         0:00.05 /Library/Application Support/Tablet/PenTabletDriver.app/Contents/Resources/ConsumerTouchDriver.app/Contents/MacOS/ConsumerTouchDriver -psn_0_114716
  501   286   215   0   0:00.01 ??         0:00.03 /Library/Application Support/Tablet/PenTabletDriver.app/Contents/Resources/TabletDriver.app/Contents/MacOS/TabletDriver -psn_0_131104
  501   565   437   0   0:00.00 ttys000    0:00.00 grep Tab

ace:Contents hongqin$ pwd

/Library/Application Support/Tablet/PenTabletDriver.app/Contents

ace:Contents hongqin$ ls ../../../Tablet/

PenTabletDriver.app PenTabletSpringboard

$ sudo mv PenTablet* /Users/hongqin/Downloads/bamboo-files-to-remove/.

After restart, the Snow Leopard laptop did not overheat again.

My learned lessons in mathematical biology (in progress)

• The key of modeling in biology is how to model the phenotype. 
• If both functions can be expanded into similar first few terms of Taylor series, they can approximate each other. This is very useful to exchange binomial form and the exponential form. 
• Initial values are very important for numerical fitting. 
• The gnls function in R often looks for local optima around the initial values. For poor data, gnls can even output the initial values as fitting results.

List of student bioinformatics programming project using python

• RE site finding
• DNA motif fining
• Phologeny parsing, display
• K-mer counting
• Reciprocal best hits
• Protein motif fining
• DNA dot-plot
• Translation of CDS to protein
• Protein MW calculation
• Yeast genome analysis
• snp inference from deep sequencing
• dn ds anlysis
• mutation inference (refer to E coli nature paper, msu's paper)
• Network permutation and aging simulation
• Possion network
• Power-law network
• Yeast PIN aging
• mitochondrial recycling
• QTL trait on aging

Verify optim() estimation using 2 and 3 parameter Gompertz model.

Using 2 and 3 parameter Gompertz model. When M is large, ignoring M will inflate I, the initial mortality rate. 




rm(list=ls())
source("/Users/hongqin/lib/R/lifespan.r")

##two parameter Gompertz model 
N=1000
I =0.005
G = 0.10
t= seq(1, 100, by=1)
s = G.s(c(I,G,0), t)
plot( s ~ t)
mu = I * exp(G*t)
plot ( s*mu ~ t )
pmf = s * mu  # prob mass function
pmf = pmf / sum(pmf)
summary ( pmf * N)
hist( round( pmf * N) )
lifespanT = rep( t, round(pmf*N))
hist(lifespanT, br=20)
summary(lifespanT)


##### log likelihood function, simple gompertz mortality model
#s = exp( (I/G) *(1 - exp(G* my.data)) )  ;
#m = I * exp( G * my.data );   
llh.gompertz.single.run <- function( IG, lifespan, trace=0 ) {
  #print(IG)
  I = IG[1]; G = IG[2]; 
  my.data = lifespan[!is.na(lifespan)];
  log_s = (I/G) *(1 - exp(G* my.data))
  #if( I< 0 ) { I = 1E-10 }
  log_m = log(I) +  G * my.data ; 
  my.lh = sum(log_s)  + sum(log_m);
  if (trace) {
    print (IG ); #trace the convergence
  }
  ret = - my.lh # because optim seems to maximize 
}

lifespan = sample(lifespanT, 30)
shat = calculate.s( lifespan )
plot(shat$s ~ shat$t )

ret1a = optim ( c(I,G)*2, fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1a$par / c(I,G)

ret1a = optim ( c(I, G), fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1a$par / c(I,G)

ret1b = optim ( c(I, G)*c(0.01, 1.5), fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1b$par / c(I,G)

ret1c = optim ( c(I,G)*c(0.01,1.5), fn=llh.gompertz.single.run, lifespan=lifespan, trace=1  );
ret1c$par / c(I, G)

ret1d = optim ( c(0.05, 0.15), fn=llh.gompertz.single.run, lifespan=lifespan, trace=1  );
ret1d$par / c(I,G)

ret1e = optim ( c(0.05, 0.1), fn=llh.gompertz.single.run, lifespan=lifespan  );
ret1e$par / ret1d$par

#################
## 3  parameter Gompertz model 
N=1000
I =0.005
G = 0.10
M = 0.05

t= seq(1, 100, by=1)
s = GM.s(c(I,G,0), t)
plot( s ~ t)

mu = I * exp(G*t) + M

plot ( s*mu ~ t )
pmf = s * mu  # prob mass function
pmf = pmf / sum(pmf)
summary ( pmf * N)
hist( round( pmf * N) )
lifespanT = rep( t, round(pmf*N))
hist(lifespanT, br=20)
summary(lifespanT)



lifespan = sample(lifespanT, 30)
shat = calculate.s( lifespan )
plot(shat$s ~ shat$t )

ret1a = optim ( c(I,G, M)*2, fn=llh.GM.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1a$par / c(I,G, M)


ret1b = optim ( c(I, G), fn=llh.G.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1b$par / c(I,G)
#ignore larger M can inflate R



ret1b = optim ( c(I, G)*c(0.01, 1.5), fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1b$par / c(I,G)

ret1c = optim ( c(I,G)*c(0.01,1.5), fn=llh.gompertz.single.run, lifespan=lifespan, trace=1  );
ret1c$par / c(I, G)

ret1d = optim ( c(0.05, 0.15), fn=llh.gompertz.single.run, lifespan=lifespan, trace=1  );
ret1d$par / c(I,G)

ret1e = optim ( c(0.05, 0.1), fn=llh.gompertz.single.run, lifespan=lifespan  );
ret1e$par / ret1d$par

Welcome email from arXiv after I registered.

The arXiv.org e-print archive is fully automated.

It processes over 200 new submissions per day.

This is only possible if YOU as author or submitter take responsibility:
always carefully check and verify your submissions, pay close attention
to diagnostic messages sent to you, and take corrective action if
necessary.

There is no secretarial staff to manually correct mistakes, fix typos,
amend layout, or perform other remedial tasks. In particular, there is
no one to guide submitters step-by-step through simple submission
procedures explained at length in the help texts, nor are there
resources to assist with generic problems of word processing software or
packaging of submissions. Use of the e-print archive is free of charge,
and this is feasible with a skeletal staff here only insofar as users
take full responsibility for their submissions.

Staff time here is dedicated to improving the software and adding
features, and tuning the server and mirror network, rather than
assisting individual users with minor problems that can be solved
entirely at the user end. It is frequently more efficient to consult a
colleague first before sending email to the server admins, so please
only email questions which are

- not explained in the online help
- cannot be solved with a little trial and error
- remain mysterious even after consulting with a computer savvy
colleague

Note that on the day of submission, before the 16:00 US Eastern time
(EDT/EST) deadline, you can replace as often as necessary to debug
layout problems interactively and to make editorial changes. There is no
penalty for multiple same day replacements and no new version number as
long as the replacements arrive here before the above daily deadline.

If despite your best efforts you cannot resolve problems with your
submission, send a concise description of the problem to
www-admin@arXiv.org, always remembering to mention the archive/papernum
or temporary identifier, and someone here will reply, typically (but not
always) within 1 working day.

DO NOT under any circumstances send your submission or any unsolicited
file attachments to www-admin. This is a group address only for
communicating e-print server related problems and suggestions. Regular
submission attempts are cached with a few day latency and we need only
the identifier you've received in order to inspect your attempted or
successful submission.

Always contact www-admin@arXiv.org if you think you have found a genuine
bug which can be reliably reproduced, and you have verified that your
web browser and display software is up to date. If a page appears not to
have been updated properly, make sure you are not looking at a page
cached by your browser or some misconfigured intermediate proxy. (Many
browsers require a SHIFT-reload to properly reload a locally cached
page.)

Thank you for your cooperation.

Symbols in R

## --- Hershey Vector Fonts

######
# create tables of vector font functionality
######
make.table <- function(nr, nc) {
    savepar <- par(mar=rep(0, 4), pty="s")
    plot(c(0, nc*2 + 1), c(0, -(nr + 1)),
         type="n", xlab="", ylab="", axes=FALSE)
    savepar
}

get.r <- function(i, nr)     i %% nr + 1
get.c <- function(i, nr)     i %/% nr + 1

draw.title <- function(title, i = 0, nr, nc) {
    r <- get.r(i, nr)
    c <- get.c(i, nr)
    text((nc*2 + 1)/2, 0, title, font=2)
}

draw.sample.cell <- function(typeface, fontindex, string, i, nr) {
    r <- get.r(i, nr)
    c <- get.c(i, nr)
    text(2*(c - 1) + 1, -r, paste(typeface, fontindex))
    text(2*c, -r, string, vfont=c(typeface, fontindex), cex=1.5)
    rect(2*(c - 1) + .5, -(r - .5), 2*c + .5, -(r + .5), border="grey")
}

draw.vf.cell <- function(typeface, fontindex, string, i, nr, raw.string=NULL) {
    r <- get.r(i, nr)
    c <- get.c(i, nr)
    if (is.null(raw.string))
        raw.string <- paste("\\", string, sep="")
    text(2*(c - 1) + 1, -r, raw.string, col="grey")
    text(2*c, -r, string, vfont=c(typeface, fontindex))
    rect(2*(c - 1) + .5, -(r - .5), (2*c + .5), -(r + .5), border="grey")
}
nr <- 25
nc <- 6
tf <- "serif"
fi <- "plain"
make.table(nr, nc)
i <- 0
draw.title("Symbol (incl. Greek) Escape Sequences", i, nr, nc)
## Greek alphabet in order
draw.vf.cell(tf, fi, "\\*A", i, nr); i<-i+1; { "Alpha"}
draw.vf.cell(tf, fi, "\\*B", i, nr); i<-i+1; { "Beta"}
draw.vf.cell(tf, fi, "\\*G", i, nr); i<-i+1; { "Gamma"}
draw.vf.cell(tf, fi, "\\*D", i, nr); i<-i+1; { "Delta"}
draw.vf.cell(tf, fi, "\\*E", i, nr); i<-i+1; { "Epsilon"}
draw.vf.cell(tf, fi, "\\*Z", i, nr); i<-i+1; { "Zeta"}
draw.vf.cell(tf, fi, "\\*Y", i, nr); i<-i+1; { "Eta"}
draw.vf.cell(tf, fi, "\\*H", i, nr); i<-i+1; { "Theta"}
draw.vf.cell(tf, fi, "\\*I", i, nr); i<-i+1; { "Iota"}
draw.vf.cell(tf, fi, "\\*K", i, nr); i<-i+1; { "Kappa"}
draw.vf.cell(tf, fi, "\\*L", i, nr); i<-i+1; { "Lambda"}
draw.vf.cell(tf, fi, "\\*M", i, nr); i<-i+1; { "Mu"}
draw.vf.cell(tf, fi, "\\*N", i, nr); i<-i+1; { "Nu"}
draw.vf.cell(tf, fi, "\\*C", i, nr); i<-i+1; { "Xi"}
draw.vf.cell(tf, fi, "\\*O", i, nr); i<-i+1; { "Omicron"}
draw.vf.cell(tf, fi, "\\*P", i, nr); i<-i+1; { "Pi"}
draw.vf.cell(tf, fi, "\\*R", i, nr); i<-i+1; { "Rho"}
draw.vf.cell(tf, fi, "\\*S", i, nr); i<-i+1; { "Sigma"}
draw.vf.cell(tf, fi, "\\*T", i, nr); i<-i+1; { "Tau"}
draw.vf.cell(tf, fi, "\\*U", i, nr); i<-i+1; { "Upsilon"}
draw.vf.cell(tf, fi, "\\+U", i, nr); i<-i+1; { "Upsilon1"}
draw.vf.cell(tf, fi, "\\*F", i, nr); i<-i+1; { "Phi"}
draw.vf.cell(tf, fi, "\\*X", i, nr); i<-i+1; { "Chi"}
draw.vf.cell(tf, fi, "\\*Q", i, nr); i<-i+1; { "Psi"}
draw.vf.cell(tf, fi, "\\*W", i, nr); i<-i+1; { "Omega"}
#
draw.vf.cell(tf, fi, "\\*a", i, nr); i<-i+1; { "alpha"}
draw.vf.cell(tf, fi, "\\*b", i, nr); i<-i+1; { "beta"}
draw.vf.cell(tf, fi, "\\*g", i, nr); i<-i+1; { "gamma"}
draw.vf.cell(tf, fi, "\\*d", i, nr); i<-i+1; { "delta"}
draw.vf.cell(tf, fi, "\\*e", i, nr); i<-i+1; { "epsilon"}
draw.vf.cell(tf, fi, "\\*z", i, nr); i<-i+1; { "zeta"}
draw.vf.cell(tf, fi, "\\*y", i, nr); i<-i+1; { "eta"}
draw.vf.cell(tf, fi, "\\*h", i, nr); i<-i+1; { "theta"}
draw.vf.cell(tf, fi, "\\+h", i, nr); i<-i+1; { "theta1"}
draw.vf.cell(tf, fi, "\\*i", i, nr); i<-i+1; { "iota"}
draw.vf.cell(tf, fi, "\\*k", i, nr); i<-i+1; { "kappa"}
draw.vf.cell(tf, fi, "\\*l", i, nr); i<-i+1; { "lambda"}
draw.vf.cell(tf, fi, "\\*m", i, nr); i<-i+1; { "mu"}
draw.vf.cell(tf, fi, "\\*n", i, nr); i<-i+1; { "nu"}
draw.vf.cell(tf, fi, "\\*c", i, nr); i<-i+1; { "xi"}
draw.vf.cell(tf, fi, "\\*o", i, nr); i<-i+1; { "omicron"}
draw.vf.cell(tf, fi, "\\*p", i, nr); i<-i+1; { "pi"}
draw.vf.cell(tf, fi, "\\*r", i, nr); i<-i+1; { "rho"}
draw.vf.cell(tf, fi, "\\*s", i, nr); i<-i+1; { "sigma"}
draw.vf.cell(tf, fi, "\\ts", i, nr); i<-i+1; { "sigma1"}
draw.vf.cell(tf, fi, "\\*t", i, nr); i<-i+1; { "tau"}
draw.vf.cell(tf, fi, "\\*u", i, nr); i<-i+1; { "upsilon"}
draw.vf.cell(tf, fi, "\\*f", i, nr); i<-i+1; { "phi"}
draw.vf.cell(tf, fi, "\\+f", i, nr); i<-i+1; { "phi1"}
draw.vf.cell(tf, fi, "\\*x", i, nr); i<-i+1; { "chi"}
draw.vf.cell(tf, fi, "\\*q", i, nr); i<-i+1; { "psi"}
draw.vf.cell(tf, fi, "\\*w", i, nr); i<-i+1; { "omega"}
draw.vf.cell(tf, fi, "\\+p", i, nr); i<-i+1; { "omega1"}
#
draw.vf.cell(tf, fi, "\\fa", i, nr); i<-i+1; { "universal"}
draw.vf.cell(tf, fi, "\\te", i, nr); i<-i+1; { "existential"}
draw.vf.cell(tf, fi, "\\st", i, nr); i<-i+1; { "suchthat"}
draw.vf.cell(tf, fi, "\\**", i, nr); i<-i+1; { "asteriskmath"}
draw.vf.cell(tf, fi, "\\=~", i, nr); i<-i+1; { "congruent"}
draw.vf.cell(tf, fi, "\\tf", i, nr); i<-i+1; { "therefore"}
draw.vf.cell(tf, fi, "\\pp", i, nr); i<-i+1; { "perpendicular"}
draw.vf.cell(tf, fi, "\\ul", i, nr); i<-i+1; { "underline"}
draw.vf.cell(tf, fi, "\\rx", i, nr); i<-i+1; { "radicalex"}

draw.vf.cell(tf, fi, "\\ap", i, nr); i<-i+1; { "similar"}
draw.vf.cell(tf, fi, "\\fm", i, nr); i<-i+1; { "minute"}
draw.vf.cell(tf, fi, "\\<=", i, nr); i<-i+1; { "lessequal"}
draw.vf.cell(tf, fi, "\\f/", i, nr); i<-i+1; { "fraction"}
draw.vf.cell(tf, fi, "\\if", i, nr); i<-i+1; { "infinity"}
draw.vf.cell(tf, fi, "\\Fn", i, nr); i<-i+1; { "florin"}
draw.vf.cell(tf, fi, "\\CL", i, nr); i<-i+1; { "club"}
draw.vf.cell(tf, fi, "\\DI", i, nr); i<-i+1; { "diamond"}
draw.vf.cell(tf, fi, "\\HE", i, nr); i<-i+1; { "heart"}
draw.vf.cell(tf, fi, "\\SP", i, nr); i<-i+1; { "spade"}
draw.vf.cell(tf, fi, "\\<>", i, nr); i<-i+1; { "arrowboth"}
draw.vf.cell(tf, fi, "\\<-", i, nr); i<-i+1; { "arrowleft"}
draw.vf.cell(tf, fi, "\\ua", i, nr); i<-i+1; { "arrowup"}
draw.vf.cell(tf, fi, "\\->", i, nr); i<-i+1; { "arrowright"}
draw.vf.cell(tf, fi, "\\da", i, nr); i<-i+1; { "arrowdown"}
draw.vf.cell(tf, fi, "\\de", i, nr); i<-i+1; { "degree"}
draw.vf.cell(tf, fi, "\\+-", i, nr); i<-i+1; { "plusminus"}
draw.vf.cell(tf, fi, "\\sd", i, nr); i<-i+1; { "second"}
draw.vf.cell(tf, fi, "\\>=", i, nr); i<-i+1; { "greaterequal"}
draw.vf.cell(tf, fi, "\\mu", i, nr); i<-i+1; { "multiply"}
draw.vf.cell(tf, fi, "\\pt", i, nr); i<-i+1; { "proportional"}
draw.vf.cell(tf, fi, "\\pd", i, nr); i<-i+1; { "partialdiff"}
draw.vf.cell(tf, fi, "\\bu", i, nr); i<-i+1; { "bullet"}
draw.vf.cell(tf, fi, "\\di", i, nr); i<-i+1; { "divide"}
draw.vf.cell(tf, fi, "\\!=", i, nr); i<-i+1; { "notequal"}
draw.vf.cell(tf, fi, "\\==", i, nr); i<-i+1; { "equivalence"}
draw.vf.cell(tf, fi, "\\~~", i, nr); i<-i+1; { "approxequal"}
draw.vf.cell(tf, fi, "\\..", i, nr); i<-i+1; { "ellipsis"}
draw.vf.cell(tf, fi, "\\an", i, nr); i<-i+1; { "arrowhorizex"}
draw.vf.cell(tf, fi, "\\CR", i, nr); i<-i+1; { "carriagereturn"}
draw.vf.cell(tf, fi, "\\Ah", i, nr); i<-i+1; { "aleph"}
draw.vf.cell(tf, fi, "\\Im", i, nr); i<-i+1; { "Ifraktur"}
draw.vf.cell(tf, fi, "\\Re", i, nr); i<-i+1; { "Rfraktur"}
draw.vf.cell(tf, fi, "\\wp", i, nr); i<-i+1; { "weierstrass"}
draw.vf.cell(tf, fi, "\\c*", i, nr); i<-i+1; { "circlemultiply"}
draw.vf.cell(tf, fi, "\\c+", i, nr); i<-i+1; { "circleplus"}
draw.vf.cell(tf, fi, "\\es", i, nr); i<-i+1; { "emptyset"}
draw.vf.cell(tf, fi, "\\ca", i, nr); i<-i+1; { "cap"}
draw.vf.cell(tf, fi, "\\cu", i, nr); i<-i+1; { "cup"}
draw.vf.cell(tf, fi, "\\SS", i, nr); i<-i+1; { "superset"}
draw.vf.cell(tf, fi, "\\ip", i, nr); i<-i+1; { "reflexsuperset"}
draw.vf.cell(tf, fi, "\\n<", i, nr); i<-i+1; { "notsubset"}
draw.vf.cell(tf, fi, "\\SB", i, nr); i<-i+1; { "subset"}
draw.vf.cell(tf, fi, "\\ib", i, nr); i<-i+1; { "reflexsubset"}
draw.vf.cell(tf, fi, "\\mo", i, nr); i<-i+1; { "element"}
draw.vf.cell(tf, fi, "\\nm", i, nr); i<-i+1; { "notelement"}
draw.vf.cell(tf, fi, "\\/_", i, nr); i<-i+1; { "angle"}
draw.vf.cell(tf, fi, "\\gr", i, nr); i<-i+1; { "nabla"}
draw.vf.cell(tf, fi, "\\rg", i, nr); i<-i+1; { "registerserif"}
draw.vf.cell(tf, fi, "\\co", i, nr); i<-i+1; { "copyrightserif"}
draw.vf.cell(tf, fi, "\\tm", i, nr); i<-i+1; { "trademarkserif"}
draw.vf.cell(tf, fi, "\\PR", i, nr); i<-i+1; { "product"}
draw.vf.cell(tf, fi, "\\sr", i, nr); i<-i+1; { "radical"}
draw.vf.cell(tf, fi, "\\md", i, nr); i<-i+1; { "dotmath"}
draw.vf.cell(tf, fi, "\\no", i, nr); i<-i+1; { "logicalnot"}
draw.vf.cell(tf, fi, "\\AN", i, nr); i<-i+1; { "logicaland"}
draw.vf.cell(tf, fi, "\\OR", i, nr); i<-i+1; { "logicalor"}
draw.vf.cell(tf, fi, "\\hA", i, nr); i<-i+1; { "arrowdblboth"}
draw.vf.cell(tf, fi, "\\lA", i, nr); i<-i+1; { "arrowdblleft"}
draw.vf.cell(tf, fi, "\\uA", i, nr); i<-i+1; { "arrowdblup"}
draw.vf.cell(tf, fi, "\\rA", i, nr); i<-i+1; { "arrowdblright"}
draw.vf.cell(tf, fi, "\\dA", i, nr); i<-i+1; { "arrowdbldown"}
draw.vf.cell(tf, fi, "\\lz", i, nr); i<-i+1; { "lozenge"}
draw.vf.cell(tf, fi, "\\la", i, nr); i<-i+1; { "angleleft"}
draw.vf.cell(tf, fi, "\\RG", i, nr); i<-i+1; { "registersans"}
draw.vf.cell(tf, fi, "\\CO", i, nr); i<-i+1; { "copyrightsans"}
draw.vf.cell(tf, fi, "\\TM", i, nr); i<-i+1; { "trademarksans"}
draw.vf.cell(tf, fi, "\\SU", i, nr); i<-i+1; { "summation"}
draw.vf.cell(tf, fi, "\\lc", i, nr); i<-i+1; { "bracketlefttp"}
draw.vf.cell(tf, fi, "\\lf", i, nr); i<-i+1; { "bracketleftbt"}
draw.vf.cell(tf, fi, "\\ra", i, nr); i<-i+1; { "angleright"}
draw.vf.cell(tf, fi, "\\is", i, nr); i<-i+1; { "integral"}
draw.vf.cell(tf, fi, "\\rc", i, nr); i<-i+1; { "bracketrighttp"}
draw.vf.cell(tf, fi, "\\rf", i, nr); i<-i+1; { "bracketrightbt"}
draw.vf.cell(tf, fi, "\\~=", i, nr); i<-i+1; { "congruent"}
draw.vf.cell(tf, fi, "\\pr", i, nr); i<-i+1; { "minute"}
draw.vf.cell(tf, fi, "\\in", i, nr); i<-i+1; { "infinity"}
draw.vf.cell(tf, fi, "\\n=", i, nr); i<-i+1; { "notequal"}
draw.vf.cell(tf, fi, "\\dl", i, nr); i<-i+1; { "nabla"}

Investigate optim() by simulation of two parameter Gompertz model

To see how optim() works in R, I tested it using simulated data. Method L-BFGS-B appears to give the most accurate fitting result. For methods tested, the initial values seem to really influence the accuracy of the fitting result.



rm(list=ls())
source("/Users/hongqin/lib/R/lifespan.r")
N=1000
I =0.005
G = 0.10
t= seq(1, 100, by=1)
s = G.s(c(I,G,0), t)
plot( s ~ t)
mu = I * exp(G*t)
plot ( s*mu ~ t )
pmf = s * mu  # prob mass function
pmf = pmf / sum(pmf)
summary ( pmf * N)
hist( round( pmf * N) )
lifespanT = rep( t, round(pmf*N))
hist(lifespanT, br=20)
summary(lifespanT)


##### log likelihood function, simple gompertz mortality model
#s = exp( (I/G) *(1 - exp(G* my.data)) )  ;
#m = I * exp( G * my.data );  
llh.gompertz.single.run <- function( IG, lifespan, trace=0 ) {
  #print(IG)
  I = IG[1]; G = IG[2];
  my.data = lifespan[!is.na(lifespan)];
  log_s = (I/G) *(1 - exp(G* my.data))
  #if( I< 0 ) { I = 1E-10 }
  log_m = log(I) +  G * my.data ;
  my.lh = sum(log_s)  + sum(log_m);
  if (trace) {
    print (IG ); #trace the convergence
  }
  ret = - my.lh # because optim seems to maximize
}

lifespan = sample(lifespanT, 30)
shat = calculate.s( lifespan )
plot(shat$s ~ shat$t )

ret1a = optim ( c(I,G)*2, fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1a$par / c(I,G)

ret1a = optim ( c(I, G), fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1a$par / c(I,G)

ret1b = optim ( c(I, G)*c(0.01, 1.5), fn=llh.gompertz.single.run, lifespan=lifespan, lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1b$par / c(I,G)

ret1c = optim ( c(I,G)*c(0.01,1.5), fn=llh.gompertz.single.run, lifespan=lifespan, trace=1  );
ret1c$par / c(I, G)

ret1d = optim ( c(0.05, 0.15), fn=llh.gompertz.single.run, lifespan=lifespan, trace=1  );
ret1d$par / c(I,G)

ret1e = optim ( c(0.05, 0.1), fn=llh.gompertz.single.run, lifespan=lifespan  );
ret1e$par / ret1d$par

R code for nested model test, likelihood ratio test, using AgingData 0517.xls

2013 Nov 6 Note: Permutation based test are probably more 'accurate' at estimating p-values than Chi-square. 


rm( list=ls())
list.files()

file = "AgingData_0517.csv"
tb = read.csv( file );


##### log likelihood function, simple gompertz mortality model
   #s = exp( (I/G) *(1 - exp(G* my.data)) )  ;
   #m = I * exp( G * my.data );  
 llh.gompertz.single.run <- function( IG, lifespan ) {
   #print(IG)
   I = IG[1]; G = IG[2];
   my.data = lifespan[!is.na(lifespan)];
   log_s = (I/G) *(1 - exp(G* my.data))
   if( I< 0 ) { I = 1E-10 }
   log_m = log(I) +  G * my.data ;
   my.lh = sum(log_s)  + sum(log_m);
   print (IG ); #trace the convergence
   ret = - my.lh # because optim seems to maximize
 }

#####

ret1a = optim ( c(0.0034, 0.1), fn=llh.gompertz.single.run, lifespan=tb[,1], lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1b = optim ( c(0.05, 0.2), fn=llh.gompertz.single.run, lifespan=tb[,1], lower=c(1E-10, 1E-5), method="L-BFGS-B" );
ret1c = optim ( c(0.039, 0.1), fn=llh.gompertz.single.run, lifespan=tb[,1]  );
ret1d = optim ( c(0.05, 0.15), fn=llh.gompertz.single.run, lifespan=tb[,1]  );
ret1c$par / ret1d$par
ret1e = optim ( c(0.1, 0.1), fn=llh.gompertz.single.run, lifespan=tb[,1]  );
ret1e$par / ret1d$par

#set up a template for fitting parameters
label = c("R","G", "mean", "median", "stddev", "CV", 'p_wilcox', 'p_ks')
allFitPar = data.frame( matrix(NA, nrow=length(label), ncol=length(tb[1,])) )
rownames(allFitPar) = label
names(allFitPar) = names(tb)

 
#loop over
for (col in names(tb)) {
  cur_lifespan = tb[,col]
  retTmp = optim ( c(0.039, 0.1), fn=llh.gompertz.single.run, lifespan=cur_lifespan  );
  allFitPar[1:2, col] = retTmp$par
  allFitPar["mean", col] = mean(cur_lifespan, na.rm=T)
  allFitPar["median", col] = median(cur_lifespan, na.rm=T)
  allFitPar["stddev", col] = sqrt( var(cur_lifespan, na.rm=T))
  allFitPar["CV", col] = allFitPar["stddev", col] / allFitPar["mean", col]
  tmp = wilcox.test( tb[,'wt'], tb[,col] ) 
  allFitPar['p_wilcox', col] = tmp$p.value
  tmp2 = ks.test( tb[,'wt'], tb[,col] ) 
  allFitPar['p_ks', col] = tmp2$p.value
 
}
allFitPar


#################################
##### LRT
### 1) model H0, same G and same I
### 2) model H1i, same G, different I
### 3) model H1g, different G, same I
### 4) model H2, different G, different I
                                  #    I1       G1       I2         G2
 H0  <- function( rawIG ) { IG <- c(rawIG[1], rawIG[2], rawIG[1], rawIG[2] ) }  #all the same
 H1i <- function( rawIG ) { IG <- c(rawIG[1], rawIG[2], rawIG[3], rawIG[2] ) }  #different I
 H1g <- function( rawIG ) { IG <- c(rawIG[1], rawIG[2], rawIG[1], rawIG[4] ) }  # different G
 H2  <- function( rawIG ) { IG <- c(rawIG[1], rawIG[2], rawIG[3], rawIG[4] ) }  # all different

 Hx.llh.gompertz.single.run <- function( rawIG, model, lifespan1, lifespan2 ) {
   IG = model(rawIG);
   I1 = IG[1]; G1 = IG[2]; I2 = IG[3]; G2 = IG[4];
   my.data1 = lifespan1[!is.na(lifespan1)];
   my.data2 = lifespan2[!is.na(lifespan2)];
   log_s1 = (I1/G1) *(1 - exp(G1* my.data1))
   log_s2 = (I2/G2) *(1 - exp(G2* my.data2))
   log_m1 = log(I1) +  G1 * my.data1 ;
   log_m2 = log(I2) +  G2 * my.data2 ;
   my.lh = sum(log_s1) + sum(log_m1) + sum(log_s2) + sum(log_m2)
   print (IG ); #trace the convergence
   ret = - my.lh # because optim seems to maximize
 }

## LRT to exam whether wt, wtCR share the same G, I
llh.H0   = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H0,   lifespan1=tb$wt, lifespan2=tb$wtCR );
llh.H1i  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1i,  lifespan1=tb$wt, lifespan2=tb$wtCR );
llh.H1g  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1g,  lifespan1=tb$wt, lifespan2=tb$wtCR );
llh.H2  = optim( c(0.01,0.2,0.01,0.1),   Hx.llh.gompertz.single.run, model=H2,  lifespan1=tb$wt, lifespan2=tb$wtCR );

cbind(llh.H0$par, llh.H1i$par, llh.H1g$par, llh.H2$par);

LH = c(llh.H0$value, llh.H1i$value, llh.H1g$value, llh.H2$value);
LH
deltaLH =  - LH + llh.H0$value;
deltaLH
1 - pchisq( 2*deltaLH, df =c(1,1,1,2) );
#p=0.06 not significant for all models.

#################################
###### End of LRT    ############
#################################

## LRT to exam whether ybr053cD, and CR share the same G, I
llh.H0   = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H0,   lifespan1=tb[,3], lifespan2=tb[,4] );
llh.H1i  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1i,  lifespan1=tb[,3], lifespan2=tb[,4] );
llh.H1g  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1g,  lifespan1=tb[,3], lifespan2=tb[,4] );
llh.H2   = optim( c(0.01,0.2,0.01,0.1),   Hx.llh.gompertz.single.run, model=H2,  lifespan1=tb[,3], lifespan2=tb[,4] );

cbind(llh.H0$par, llh.H1i$par, llh.H1g$par, llh.H2$par);

LH = c(llh.H0$value, llh.H1i$value, llh.H1g$value, llh.H2$value);
LH
deltaLH =  - LH + llh.H0$value;
deltaLH
1 - pchisq( 2*deltaLH, df =c(1,1,1,2) );
#[1] 1.00000000 0.01498437 0.01368829 0.04515191

#################################
###### End of LRT    ############
#################################

## LRT to exam whether ybr053cD, and CR share the same G, I
llh.H0   = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H0,   lifespan1=tb[,5], lifespan2=tb[,6] );
llh.H1i  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1i,  lifespan1=tb[,5], lifespan2=tb[,6] );
llh.H1g  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1g,  lifespan1=tb[,5], lifespan2=tb[,6] );
llh.H2   = optim( c(0.01,0.2,0.01,0.1),   Hx.llh.gompertz.single.run, model=H2,  lifespan1=tb[,5], lifespan2=tb[,6] );
cbind(llh.H0$par, llh.H1i$par, llh.H1g$par, llh.H2$par);

LH = c(llh.H0$value, llh.H1i$value, llh.H1g$value, llh.H2$value);
LH
deltaLH =  - LH + llh.H0$value;
deltaLH
1 - pchisq( 2*deltaLH, df =c(1,1,1,2) );
#[1] 1.00000000 0.04595566 0.31817030 0.04188332

#################################
###### End of LRT    ############
#################################


## LRT to exam whether ybr053cD, and CR share the same G, I
llh.H0   = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H0,   lifespan1=tb[,7], lifespan2=tb[,8] );
llh.H1i  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1i,  lifespan1=tb[,7], lifespan2=tb[,8] );
llh.H1g  = optim( c(0.01,0.2,0.01,0.1),  Hx.llh.gompertz.single.run, model=H1g,  lifespan1=tb[,7], lifespan2=tb[,8] );
llh.H2   = optim( c(0.01,0.2,0.01,0.1),   Hx.llh.gompertz.single.run, model=H2,  lifespan1=tb[,7], lifespan2=tb[,8] );

cbind(llh.H0$par, llh.H1i$par, llh.H1g$par, llh.H2$par);

LH = c(llh.H0$value, llh.H1i$value, llh.H1g$value, llh.H2$value);
LH
deltaLH =  - LH + llh.H0$value;
deltaLH
1 - pchisq( 2*deltaLH, df =c(1,1,1,2) );
#[1] 1.00000000 0.04595566 0.31817030 0.04188332

#################################
###### End of LRT    ############
#################################